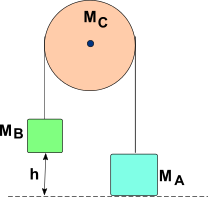
Macchina di Atwood

Non e’ altro che una carrucola di massa M che puo’ ruotare senza attrito attorno ad un asse orizzontale passante per il suo centro

Vogliamo sollevare la massa M_B tramite la massa M_A , ovviamente deve essere M_A > M_B

Sappiamo risolvere questo problema se la carrucola ha massa trascurabile. Ora, invece la carrucola ha una sua massa M_C che ruota, quindi lo dobbiamo considerare come un sistema in rotazione.

Dopo la rotazione M_B e’ salita della quantita’ h, M_A e’ scesa della stessa quantita’ e la ruota ha girato a velocita’ angolare ω. Le domande tipiche per problemi di questo tipo sono

– Accelerazione del sistema

– Velocita’ di impatto di M_A o velocita’ di M_B (sono uguali dato che sono collegate)

– Tensioni della fune

– Velocita’ angolare massima

Notiamo subito alcune cose, la fune presenta tensioni diverse, ossia ci sono zone piu’ tese e zone meno tese della corda Se la tensione a sinistra fosse uguale a quella di destra la ruota non girerebbe. La velocita’ angolare della carrucola e’ legata alla velocita’ delle masse perche’ M_C ruota mentre M_B e M_A salgono e scendono.

Per il nostro studio consideriamo una situazione intermedia, M_A sta’ scendendo e M_B sta’ salendo.

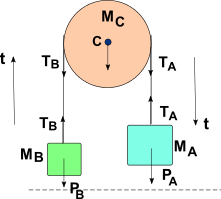Per la massa M_A , lungo l’asse t possiamo porre

P_A – T_A = M_A a_A

Per la massa M_B lungo l’asse t poniamo

T_B – P_B = M_B a_B

Dato che a_A = a_B = a

$\displaystyle{\begin{cases}\textbf{ P}_A-\textbf{T}_A=\textbf{M}_A\, \textbf{a} \\ \textbf{T}_B-\textbf{P}_B=\textbf{M}_B\,\textbf{a}\end{cases}}$

Vediamo la rotazione della carrucola

Per quanto riguarda la prima equazione cardinale, considerando ad esempio come assi X e Y abbiamo

asse Y : R_C= P_C + T_A + T_B

asse X : 0 = 0 non c’e’ niente lungo questo asse

Dall’equazione lungo Y possiamo ricavarci la reazione del cardine. Il cardine deve reggere il peso e le due tensioni.

Seconda equazione cardinale

$\displaystyle{\mathbf{M^{est}=I_C\,\frac{d\omega}{dt}}}$

Le forze presenti sulla carrucola sono la forza peso P_C , la reazione del cardine R_C , le tensioni T_A e T_B

$\displaystyle{\mathbf{M^{est}=M^{est}_{P_C}+M^{est}_{R_C}+M^{est}_{T_A}+M^{est}_{t_B}=I_C\, \frac{d\omega}{dt}}}$

I momenti devono produrre l’accelerazione angolare del sistema. Andiamo a valutare questi quattro momenti.

Il momento della reazione del cardine M_Rc e’ nullo perche’ la forza non ha braccio, sta’ proprio sull’asse di rotazione.

Il momento della forza peso e’ nullo per lo stesso motivo

Dato che abbiamo posto M_A > M_B il sistema ruota in senso orario. Nulla ci vieta di considerare positivi i momenti che aiutano la rotazione

M_TA = T_A r

M_TAB = – T_B r

r e’ la distanza di T_A e T_B dall’asse di rotazione

Per il momento totale delle forze esterne abbiamo

$\displaystyle{\mathbf{T_A\, r-T_B\, r=I_C\,\frac{d\omega}{dt}\;\longrightarrow\, r(T_A-T_B)=I_C\,\frac{d\omega}{dt}}}$ .

$\displaystyle{\mathbf{T_A-T_B=\frac{I_C}{r}\,\frac{d\omega}{dt}}}$

Da questa relazione e’ chiaro che se fosse T_A = T_Bnon ci sarebbe accelerazione angolare. La ruota accelera se c’e’ differenza di tensione.

Vogliamo ora stabile una relazione tra la rotazione della carrucola (della ruota) e lo scorrimento della fune. Dobbiamo sincronizzare la salita e la discesa delle masse con la ruota che gira. Consideriamo allora il punto di contatto tra fune e ruota

Nel punto che stiamo considerando abbiamo la fune che ha velocita’ V_fune che e’ una velocita’ lineare, abbiamo la ruota che ha velocita’ ω r dove r e’ il raggio della ruota. C’e’ pero’ anche l’attrito che si oppone al movimento relativo tra fune e ruota. Questo attrito e’ A_S , e’ un attrito statico perche’ in quel punto stanno attaccate fune e ruota. Considerando che V e ω variano nel tempo, in quel punto possiamo porre

V_fune(t) = ω(t) r

Se deriviamo questa relazione otteniamo l’accelerazione della fune

$\displaystyle{\mathbf{a_{fune}=\frac{dv}{dt}=r\,\frac{d\omega}{dt}=\alpha r}}$

dove α e’ l’accelerazione angolare della ruota. L’attrito fa’ si’ che l’accelerazione della fune sia legata all’accelerazione angolare della ruota. Mettendo questo risultato nell’equazione di prima si ha

$\displaystyle{\mathbf{T_A-T_B=\frac{I_C}{r}\,\frac{d\omega}{dt}=\frac{I_C}{r^2}\, a}}$

In luogo di dω/dt abbiamo messo a/r

Prendiamo tutte le equazioni stabilite

$\displaystyle{\begin{cases} \textbf{P}_A-\textbf{T}_A=\textbf{M}_A\, \textbf{a}\\ \textbf{T}_B-\textbf{P}_B=\textbf{M}_B\, \textbf{a} \\ \textbf{T}_A-\textbf{T}_B=\frac{\textbf{I}_C}{\textbf{r}^2}\, \textbf{a}\end{cases}}$

e le sommiamo membro a membro

$\displaystyle{\mathbf{P_A-P_B=\left (M_A+M_B+\frac{I_C}{r^2}\right )\, a}}$

Al posto della forza peso mettiamo la sua espressione P = M g

$\displaystyle{\mathbf{(M_A-M_B)\, g=\left (M_A+M_B+\frac{I_C}{r^2}\right )\, a\; \longrightarrow\; a=g\,\frac{M_A-M_B}{M_A+M_B+\frac{I_C}{r^2}}}}$

Se la ruota e’ piena I_C = 1/2 M_C r² e’ il momento d’inerzia di un disco pieno che ruota attorno ad un asse per il suo centro

$\displaystyle{\mathbf{a=g\,\frac{M_A-M_B}{M_A+M_B+\frac{1}{2}M_C}}}$

La ruota fa’ da zavorra, l’accelerazione e’ < di g quindi possiamo spostare grandi pesi lentamente.

Una volta calcolata l’accelerazione trovare le tensioni della fune e’ semplice, basta riprendere le equazioni iniziali

$\displaystyle{\mathbf{P_A-T_A=M_A\, a\;\longrightarrow\;T_A=P_A-M_A\, a=M_A\, g-M_A\, a=M_A(g-a)=M_A\, g\left (\frac{2M_B+\frac{M_C}{2}}{M_A+M_B+\frac{M_C}{2}}\right )}}$

Stessa cosa per la tensione T_B

$\displaystyle{\mathbf{T_B=M_B(a+g)=M_B\, g\left (\frac{2M_A+\frac{M_C}{2}}{M_A+M_B+\frac{M_C}{2}}\right )}}$

Per trovare la velocita’ con cui M_A arriva a terra ci serve il tempo impiegato. Sappiamo che

V = a t che S = 1/2 a t² e che la massa arriva a terra quando S = h

$\displaystyle{\mathbf{h=\frac{1}{2}at^2\;\longrightarrow\;t=\sqrt{\frac{2h}{a}}}}$

Il tempo lo mettiamo nell’espressione di V

$\displaystyle{\mathbf{v=at=a\sqrt{\frac{2h}{a}}=\sqrt{2ha}=\sqrt{2gh}\,\sqrt{\frac{M_A-M_B}{M_A+M_B+\frac{M_C}{2}}}}}$

Nella prossima lezione studiamo la macchina di Atwood con considerazioni energetiche.

I like physics

Macchina di Atwood

Prossima lezione Macchina di Atwood con considerazioni energetiche