Capacità di un condensatore con due dielettrici

Vediamo la capacità di un condensatore con due dielettrici.

Iniziamo dal caso di dielettrici sovrapposti.

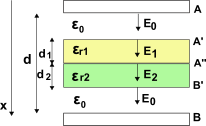Questo è il nostro condensatore con due dielettrici, di costanti dielettriche ε_r1e ε_r2 rispettivamente, messi l’uno sull’altro. Partiamo dal caso generale in cui la distanza tra le armature è d e lo spessore dei dielettrici, d₁e d₂, non riempie tutto lo spazio.

Questo sistema può essere considerato come due condensatori in serie di capacità

$\displaystyle{\mathbf{\frac{1}{C_S}=\frac{1}{C_1}+\frac{1}{C_2}}}$

che, nel caso di due condensatori, può essere scritta

$\displaystyle{\mathbf{C_S=\frac{C_1C_2}{C_1+C_2}}}$

Dimostriamo che quanto detto è vero. Partiamo dalla capacità di un condensatore, sappiamo che essa è data dal rapporto tra la carica allocata sulle armature, Q_lib, e la differenza di potenziale tra le armature.

$\displaystyle{\mathbf{C=\frac{Q_{lib}}{V_A-V_B}}}$

La carica sull’armatura è pari alla densità superficiale σ_lib(l’armatura è fatta di materiale conduttore e le cariche si dispongono sulla superficie) moltiplicata per la superficie S dell’armatura.

$\displaystyle{\mathbf{C=\frac{Q_{lib}}{V_A-V_B}=\frac{\sigma_{lib}\, S}{V_A-V_B}}}$

Dobbiamo esprimere la differenza di potenziale, lo facciamo come al solito integrando il campo elettrico lungo un percorso che va da A a B. Dobbiamo fare attenzione perchè esso si divide in quattro parti. Nel tratto AA’ il percorso avviene nel vuoto, da A’ a A” nel dielettrico 1, da A” a B’ nel dielettrico 2 e, infine, da B’ a B di nuovo nel vuoto.

$\displaystyle{\mathbf{V_A-V_B=\int_A^{A'}E_o\, dx+\int_{A'}^{A''}E_1\, dx+\int_{A''}^{B'}E_2\, dx+\int_{B'}^BE_o\, dx}}$

Risolviamo questi integrali

$\displaystyle{\mathbf{\int_A^{A'}E_o\, dx+\int_{B'}^BE_o\, dx=E_o(d-d_1-d_2)}}$

Il vuoto, dove il campo elettrico è E_o, è presente nel tratto d-d1-d2, dove non ci sono i dielettrici.

$\displaystyle{\mathbf{\int_{A'}^{A''}E_1\, dx=E_1 d_1}}$

d1 è il tratto dove il campo vale E₁

$\displaystyle{\mathbf{\int_{A''}^{B'}E_2\, dx=E_2 d_2}}$

Nel tratto d₂ il campo presente è E₂

Sostituiamo il tutto nella differenza di potenziale

$\displaystyle{\mathbf{V_A-V_B=E_o(d-d_1-d_2)+E_1\, d_1+E_2\, d_2}}$

Esprimiamo i vari campi elettrici

$\displaystyle{\mathbf{E_o=\frac{\sigma_{lib}}{\epsilon_o}\,\qquad\, E_1=\frac{\sigma_{lib}}{\epsilon_o\, \epsilon_{r1}}\,\qquad\, E_2=\frac{\sigma_{lib}}{\epsilon_o\, \epsilon_{r2}}}}$

Di nuovo sostituiamo

$\displaystyle{\mathbf{V_A-V_B=\frac{\sigma_{lib}}{\epsilon_o}\, (d-d_1-d_2)+\frac{\sigma_{lib}}{\epsilon_o\, \epsilon_{r1}}\, d_1+\frac{\sigma_{lib}}{\epsilon_o\, \epsilon_{r2}}\, d_2}}$ .

$\displaystyle{\mathbf{V_A-V_B=\frac{\sigma_{lib}}{\epsilon_o}\,\Biggl [d-(d_1+d_2)+\frac{d_1}{\epsilon_{r1}}+\frac{d_2}{\epsilon_{r2}}\Biggr ]}}$ .

se sostituite questa espressione in quella di partenza di C trovate la capacità di un condensatore con due dielettrici con in più anche spazio vuoto.

Per andare avanti agevolmente, facciamo il caso in cui i dielettrici riempiono tutto lo spazio tra le due armature, d = d1 + d2.

$\displaystyle{\mathbf{V_A-V_B=\frac{\sigma_{lib}}{\epsilon_o}\Biggl (\frac{d_1}{\epsilon_{r1}}+\frac{d_2}{\epsilon_{r2}}\Biggr )}}$

Finalmente possiamo calcolare la capacità di questo condensatore

$\displaystyle{\mathbf{C=\frac{\sigma_{lib}\, S}{V_A-V_B}=\cfrac{\epsilon_o\, S}{\cfrac{d_1}{\epsilon_{r1}}+\cfrac{d_2}{\epsilon_{r2}}}}}$

Se prendiamo due condensatori , uno contenente il dielettrico 1 e l’altro il dielettrico 2 e li poniamo in serie

$\displaystyle{\mathbf{C_1=\frac{\epsilon_o\,\epsilon_{r1}\, S}{d1}\,\qquad\, C_2=\frac{\epsilon_o\,\epsilon_{r2}\, S}{d2}}}$ .

$\displaystyle{\mathbf{C=\frac{C_1C_2}{C_1+C_2}}}$

Vi torna esattamente l’espressione trovata prima per la capacità di un condensatore con due dielettrici.

Passiamo ora al caso di due dielettrici affiancati.

Ora la superficie di separazione dei due dielettrici è in verticale.

Se la configurazione vista prima era di tipo serie è facile dire che questa è parallela, infatti il sistema di figura equivale a due condensatori in parallelo.

Avrete notato che le cariche libere sulle armature non sono disegnate equispaziate, perchè ?. Essendo i due dielettrici diversi, si polarizzano in maniera differente. Il dielettrico che si polarizza di più presenterà più cariche negative sulla superficie superiore è più cariche positive su quella inferiore, rispetto all’altro dielettrico.

Ricordiamo che la polarizzazione avviene tramite la formazione di tantissimi dipoli in modo tale che, alla fine, vediamo un addensamento di carica in alto e una in basso nel dielettrico.

Il dielettrico che presenta un maggior numero di cariche negative attrae le cariche positive libere creando una distribuzione non uniforme.

Quello che è uguale per i due dielettrici è la differenza di potenziale V_A– V_B .

Scriviamo i campi elettrici nei due dielettrici

$\displaystyle{\mathbf{E_1=\frac{V_A-V_B}{d}}}$ .

$\displaystyle{\mathbf{E_2=\frac{V_A-V_B}{d}}}$ .

V_A– V_B è sempre la stessa, la distanza d tra le armature pure, ne deduciamo che :

$\displaystyle{\mathbf{E_1=E_2}}$

I campi elettrici nei due mezzi sono uguali. Se ε_r1≠ ε_r2come è possibile ? Semplice :

$\displaystyle{\mathbf{E_1=\frac{\sigma_{lib1}}{\epsilon_o\,\epsilon_{r1}}\,\qquad\, E_2=\frac{\sigma_{lib2}}{\epsilon_o\,\epsilon_{r2}} }}$

Vuol dire che, come affermato prima solo concettualmente, σ_lib1≠ σ_lib2 .

Le cariche libere si dispongono in modo non uniforme.

Passiamo al vettore spostamento elettrico nei due mezzi dielettrici

$\displaystyle{\mathbf{D_1=\epsilon_o\,\epsilon_{r1}\, E_1=\epsilon_o\,\epsilon_{r1}\,\frac{\Delta V}{d}}}$ .

$\displaystyle{\mathbf{D_2=\epsilon_o\,\epsilon_{r2}\, E_2=\epsilon_o\,\epsilon_{r2}\,\frac{\Delta V}{d}}}$

Ma, se ricordate che

$\displaystyle{\mathbf{D_1=\sigma_{lib1}\,\qquad\, D_2=\sigma_{lib2}}}$

facendo il rapporta D1 su D2

$\displaystyle{\mathbf{\frac{D_1}{D_2}=\frac{\sigma_{lib1}}{\sigma_{lib2}}=\cfrac{\epsilon_o\,\epsilon_{r1}\,\cfrac{\Delta V}{d}}{\epsilon_o\,\epsilon_{r2}\,\cfrac{\Delta V}{d}}=\frac{\epsilon_{r1}}{\epsilon_{r2}}}}$ .

$\displaystyle{\mathbf{\frac{\sigma_{lib1}}{\sigma_{lib2}}=\frac{\epsilon_{r1}}{\epsilon_{r2}}}}$ .

Ecco la relazione di cui abbiamo parlato sino ad ora.

A questo punto troviamo anche il rapporto le distribuzioni di carica di polarizzazione.

Quando abbiamo studiato le cariche di polarizzazione in un condensatore siamo giunti alla relazione

$\displaystyle{\mathbf{\frac{\sigma_{pol}}{\sigma_{lib}}=\frac{\epsilon_r-1}{\epsilon_r}\,\Longrightarrow\, \sigma_{pol}=\frac{\epsilon_r-1}{\epsilon_r}\,\sigma_{lib}}}$

Allora

$\displaystyle{\mathbf{\frac{\sigma_{pol1}}{\sigma_{pol2}}=\cfrac{\cfrac {\epsilon_{r1}-1}{\epsilon_{r1}}}{\cfrac{\epsilon_{r2}-1}{\epsilon_{r2}}}\,\,\,\frac{\sigma_{lib1}}{\sigma_{lib2}}= \cfrac{\cfrac {\epsilon_{r1}-1}{\epsilon_{r1}}}{\cfrac{\epsilon_{r2}-1}{\epsilon_{r2}}}\,\,\,\frac{\epsilon_{r1}}{\epsilon_{r2}} }}$ .

$\displaystyle{\mathbf{\frac{\sigma_{pol1}}{\sigma_{pol2}}=\frac{\epsilon_{r1}-1}{\epsilon_{r2}-1}}}$

La densità di carica di polarizzazione non è uniforme.

Il mezzo con costante dielettrica maggiore si carica con maggiore densità di carica di polarizzazione e richiama più carica libera.

Non abbiamo ancora finito, ci resta da calcolare la capacità di questo condensatore.

Dividiamo la sezione A dell’armatura in due parti. Una, che chiamiamo S1 è quella sopra il dielettrico 1, l’altra, S2 è quella sovrapposta al dielettrico 2.

La capacità è sempre

$\displaystyle{\mathbf{C=\frac{Q_{lib}}{\Delta V}}}$

La carica libera è distribuita in parte su S1 è in parte su S2.

$\displaystyle{\mathbf{Q_{lib1}=\sigma_{lib1}\, S_1}}$ .

$\displaystyle{\mathbf{Q_{lib2}=\sigma_{lib2}\, S_2}}$

Sostituiamo nella capacità

$\displaystyle{\mathbf{C=\frac{\sigma_{lib1}\, S_1+\sigma_{lib2}\, S_2}{\Delta V}=\frac{\sigma_{lib1}\, S_1}{\Delta V}+\frac{\sigma_{lib2}\, S_2}{\Delta V}=C_1+C_2}}$

Un condensatore con due dielettrici aventi superficie di separazione in verticale, lo possiamo vedere come due condensatori in parallelo.

Finalmente abbiamo finito !